Verification vs. Validation
There are many types of models and many ways to verify and validate those models. This article provides a discussion of verification and validation using the context of creating a digital model to simulate, analyze, and optimize a physical production system.
There are 3 important components to every model – 1) the real-world system, 2) the conceptual model, and 3) the production system model. The real-world system is the physical system that is responsible for producing some goods or services for a set of customers. The production system model is a digital twin that is built in computer software to study the real-world system and test potential changes to the system for overall system improvement. A conceptual model is a non-software specific description of the computer simulation model (that will be, is or has been developed), describing the objectives, inputs, outputs, content, assumptions, and simplifications of the model. (Robinson 2008a)

The basic structure used in the Production Optimizer Conceptual Model describes a process as follows. A company is composed of flows and items. Flows are collections of routings. Items are assigned to routings. Routings have process steps arranged in a routing sequence. Process steps have resources. A resource can be a machine, or a resource can be labor.

Verification
The purpose of creating a model is to experiment quickly and safely on a complex physical system that would otherwise be expensive and risky to test on. Therefore, the model must be tested to ensure it is a reliable, precise, and accurate representation of the physical system. Each model must undergo a verification and validation process.
The purpose of verification is to confirm that the model has been constructed correctly with respect to the conceptual model. A verified model will produce results consistent with what is expected using the input parameters. If the results of the model match the expectation, then the modeler can move on to validation. Model verification does not compare computed results to the real world system. That is the purpose of validation.
Validation
The purpose of validation is to ensure trust in the production system model. Trust is gained with a model that produces results that are consistent with the historical performance of the real system. Validation is the process of comparing historical performance with the performance of the model. Since this process relies on data collected from the real system, validation can get difficult if real data is not available. In this case, the modeler can compare real system behavior with model behavior.
In nearly all cases, the first version of a model shows results different than what you have historically seen as actual results. The iterations that are required to make changes to the model and test your assumptions about the value stream provide a wealth of information about your value stream. The information (run rates, set-up time, WIP levels, etc.) is typically spread among numerous people that work with the value stream. The model provides a convenient structure for pulling all the information together. This structure provides value stream managers and workers a practical method for getting their minds around the value stream to clarify and simplify performance improvement.
Verify Capacity Utilization
There is always a bit of art in applying the principles of Operations Science to modeling. The steps described below are those typically taken by modeling experts for model verification but there are different options for verifying model results and the steps described below should not be interpreted as being the only way to use the Production Optimizer to analyze processes.
- Check Capacity Utilization
- Capacity Utilization is calculated as Time Used / Time Available.
Capacity Utilization is calculated as Time Used divided by Time Available. In most cases, Time Available does not include all day every day. There is typically a policy in place that limits Time Available to somewhere in the range of 40 – 80 hours per week per resource.

Each process center is assigned a schedule (working calendar) discussed in an earlier section of this help menu. The working calendar represents the total time that a single process center has available to work in a week. If there are multiple process centers of the same type available, the total time available is multiplied by the number of parallel process centers. This calculation is the same for work groups and the resource pool.
To calculate Time Used, the modeler must calculate Raw Process Time for a transfer batch. Raw process time includes Process Time, Setup Time, and Outages (downtime). The Production Optimizer does not count Move Time as an operation that places load on Process Centers, Work Groups and Resource Pool. If Move Time is performed by one of the resource groups below, it should be factored into a process step.
If move time exists it will be shown separately from raw process time cycle time analysis section of the results page.
A transfer batch is…

RPT is calculated as follows:
- Qp = Process batch size
- Qt = Transfer batch size
- S = setup time (for a process batch, there is no setup for a transfer batch unless process batch size = transfer batch size)
- t0 = nominal process time
- A = Availability
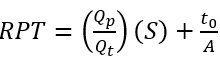
Once RPT is known, Time Used is calculated as follows:
- RPT = Raw Process Time for a single transfer batch
- n = number of transfer batches scheduled during Time Available
Time Used = (n)(RPT)
In the airplane assembly example, there is a demand of 10 airplanes per week. There is only one routing and 100% of the demand for airplanes goes through the single routing. Each of the 5 process steps is assigned to a different process center. Therefore, in a single week, each process center is used for the length of the process time for its allocated process step multiplied by 10 airplanes. For example, WS-4 is assigned to the “Install Engines” process step. That process step has a rate of 0.05 airplanes per hour, or 20 hours per airplane. With a demand of 10 airplanes per week, the total time used for this process center is 200 hours.
WS-4 uses a 2x7x12 working calendar. Two shifts per day, 7 days per week, and 12 hours per shift returns 168 working hours of time available. There is no downtime in this example. Therefore, the modeler should expect to see a capacity utilization of 200 hours / 168 hours or 119.04%.
To verify capacity utilization, the modeler can look at the Capacity Utilization chart at the top of the results page or scroll down to the table with capacity utilization data. If utilization values for each resource align with the modeler’s calculation, the model can be considered verified.

Verify Raw Process Times
To ensure that process rates / process times were input correctly, the user can calculate raw process times (RPT). In the airplane assembly example, there are 5 process steps. Step 1, 2, 3, 4 and 5 have average process times of 3.2 hours, 14 hours, 15 hours, 20 hours, and 9.6 hours. Therefore RPT = 5 * (3.2 + 14 + 15 + 16 + 9.6) = 289 hours. This matches the screenshot of the model results below.

Validate a Model
Typically, the model performs better than the real system, the first time it is built. There is an iterative process of comparing results with observed performance and adjusting input data. When validating a model against actual performance, the modeler should keep track of the changes made to the model to get the model to match actual performance. The changes represent opportunities for improvement in practice and serve as guides on how to proceed in implementing changes in practice.
Since validation involves comparing model performance with actual historical performance, the process can become challenging when no historical data is available. The following table provides validation methods for processes with data available or not.
| Modeling Scenario | Validation Method |
|---|---|
| Existing process with available data | Test model in normal and extreme cases. Compare capacity utilization, throughput, WIP and cycle times. |
| Existing process with no available data | Compare behaviors of real process with the model |
| Non-existing process with known relationship of variables | Correlation analysis to compare outcome of the model with the input variables. Compare to the known relationship of the variables. |
Compare Capacity Utilization
Most organizations do not keep track of capacity utilization over time. Therefore, this can be difficult to validate with data. However, if a production system is running and keeping up with demand, it should not have any resources with a capacity utilization exceeding 100%. Therefore when modeling this system, the model should not indicate a resource with capacity utilization greater than 100%. If it does, then one or more of the parameters that drive utilization must be adjusted. Conversely, if a system is falling behind, then it is likely that one or more resources have a capacity utilization close to or greater than 100%. In this case, compare observed performance of each resource with the utilization calculated by the model.
Compare Throughput, WIP and Cycle Time
Unless the system does not exist, actual throughput data is typically easy to get. This is just a record of what got done over a period of time. It’s important to note here that “what got done”, means what was 100% finished. Throughput is not a measure of partially completed items or scopes of work.
Actual WIP and cycle time information require that there is documentation capturing when an item or scope of work starts and when it finishes. The difference between those finish dates/times and start dates/times represents the cycle time. WIP can be calculated by accumulating of how many starts there are over time and deducting the number of completions from that cumulative value.
The simplest way to validate a model with these measurements is to plot them on a chart. If the actual performance and the modeled performance align closely, the model can be trusted as a valid means to predict system performance. If there are large discrepancies, the model will need to be adjusted and this process repeated. For example, the figure below illustrates the difference between a model is a good match for comparing throughput (Left) versus a poor match (Right).
